Основи програмування

Мета роботи: ознайомитися з існуючими алгоритмами сортування інформації.

Теоретичні відомості

Алгоритм сортування – це алгоритм, що розв’язує задачу сортування, тобто здійснює впорядкування лінійного списку (масиву) елементів.

Вхід алгоритму: послідовність з n чисел (a₁, a₂, ..., a_n)

Вихід алгоритму: перестановка (a_π(1), a_π(2), ..., a_π ) вхідної послідовності таким чином, що a_π(1) ≤ a_π(2)  ≤ ... ≤a_π  (π - перестановка послідовності 1 ... n).

Вхідна послідовність найчастіше представляється у вигляді масиву.

Найбільш відомі алгоритми сортування:

• Сортування обміном (сортування бульбашкою) – для кожної пари індексів проводиться обмін, якщо елементи розташовані не по порядку.
• Сортування вибором – пошук найменшого або найбільшого елемента і переміщення його на початок або в кінець впорядкованого списку.
• Сортування вставкою – визначаємо місце де поточний елемент повинен знаходитися у впорядкованому списку, і вставляємо його туди.

Сортування методом «бульбашки»

Сортування обміном або сортування «бульбашкою» є простим алгоритмом сортування. Алгоритм працює таким чином – у поданому наборі даних (списку чи масиві) порівнюються два сусідні елементи. Якщо один з елементів, не відповідає критерію сортування (є більшим, або ж, навпаки, меншим за свого сусіда), то ці два елементи міняються місцями. Прохід по списку продовжується до тих пір, доки дані не будуть відсортованими. Алгоритм отримав свою назву від того, що процес сортування за ним нагадує поведінку бульбашок повітря у резервуарі з водою. Оскільки для роботи з елементами масиву він використовує лише порівняння, це сортування на основі порівнянь.

Візьмемо масив чисел «5 1 4 2 8», і за допомогою даного алгоритму, відсортуємо його від найменшого до найбільшого елементу. На кожному кроці, елементи, виділені іншим кольором будуть порівнюватись. Перший прохід:

(5 1 4 2 8) → (1 5 4 2 8)

Тут, алгоритм порівнює перші два елементи, і міняє їх місцями.

(1 5 4 2 8) → (1 4 5 2 8)

(1 4 5 2 8) → (1 4 2 5 8)

(1 4 2 5 8) → (1 4 2 5 8)

Тут порівнювані елементи знаходяться на своїх місцях, тож алгоритм не міняє їх місцями. Другий прохід:

(1 4 2 5 | 8) → (1 4 2 5 | 8)

(1 4 2 5 | 8) → (1 2 4 5 | 8)

(1 2 4 5 | 8) → (1 2 4 5 | 8)

Тепер наш масив повністю відсортований, однак, алгоритм цього ще не знає. Йому потрібен ще один «пустий» прохід, під час якого він не поміняє місцями жодного елементу. Третій прохід:

(1 2 4 | 5 8) → (1 2 4 | 5 8)

(1 2 4 | 5 8) → (1 2 4 | 5 8)

Нарешті, масив відсортовано, і алгоритм може припинити свою роботу.

Алгоритм можна виразити наступним чином:

процедура бульбашка(A: список елементів придатних для сортування)

   повторювати    

     переставлені = неправда

     для i = 1 включно до довжина(A) - 1 робити:

       /* якщо ця пара невпорядкована */

       якщо A[i-1] > A[i] тоді

         /* поміняти місцями і запам'ятати, що щось змінилось */

         переставити( A[i-1], A[i] )

         переставлені = істина

       кінець якщо

     кінець для

   доки не переставлені

кінець процедури

Розглянемо приклад програми Bubbles, яка сортує одновимірний масив цілих чисел методом «бульбашки» (рис. 5.1):

  

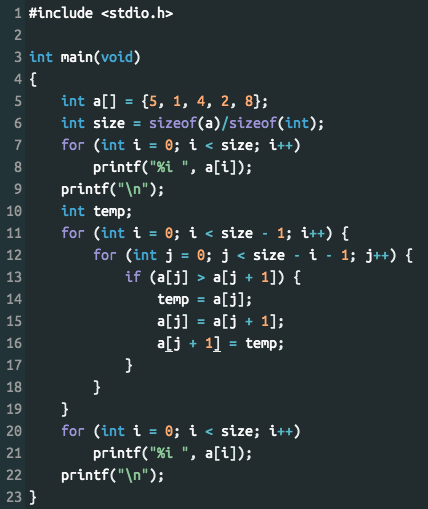
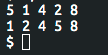
Рисунок 5.1 – Код програми Bubbles та результат її виконання

На першому кроці (рис. 5.1, рядок 5) відбувається оголошення масиву та заповнення його значеннями. Далі відбувається визначення його розміру (рис. 5.1, рядок 6), для цього потрібно визначити розмір масиву в байтах (оператор sizeof) та поділити його на розмір типу даних в байтах (в даному випадку – int).

Сам алгоритм сортування представлений у вигляді коду, показаного в рядках 11-19 на рисунку 5.1.

Сортування включенням

Сортування включенням – простий алгоритм сортування на основі порівнянь.

Наприклад, більшість людей при сортуванні колоди гральних карт, використовують метод, схожий на алгоритм сортування включенням.

На кожному кроці алгоритму вибирається один з елементів вхідних даних і вставляється на потрібну позицію у вже відсортованому списку до тих пір, доки набір вхідних даних не буде вичерпано. Метод вибору чергового елементу з початкового масиву довільний; може використовуватися практично будь-який алгоритм вибору.

Сортування вибором

Сортування вибором – простий алгоритм сортування лінійного масиву, на основі вставок. Сортування вибором вирізняється більшою простотою, ніж сортування включенням, і в деяких випадках, вищою продуктивністю.

Алгоритм працює таким чином:

1. Знаходить у списку найменше значення
2. Міняє його місцями із першим значеннями у списку
3. Повторює два попередніх кроки, доки список не завершиться (починаючи з другої позиції)

Фактично, таким чином список ділиться на дві частини: перша (ліва) – повністю відсортована, а друга (права) – ні.

Ось приклад сортування масиву з п'яти елементів за даним алгоритмом:

64 25 12 22 11

11 25 12 22 64

 

11 | 25 12 22 64

11 | 12 25 22 64

 

11 12 | 25 22 64

11 12 | 22 25 64

Сортування вставками

Сортування вставками також може працювати зі списками, які підтримують операції додавання і видалення. В такому разі, більш зручно видаляти зі списку найменший елемент, і вставляти його в кінець відсортованої частини масиву. Наприклад:

| 64 25 12 22 11

11 | 64 25 12 22

11 12 | 64 25 22

11 12 22 | 64 25

11 12 22 25 | 64

Сортування злиттям

В основі цього алгоритму сортування лежить злиття двох впорядкованих ділянок масиву в одну впорядковану ділянку іншого масиву.

Під час сортування в дві допоміжні черги з основної поміщаються перші дві відсортовані підпослідовності, які потім зливаються в одну і результат записується в тимчасову чергу. Потім з основної черги беруться наступні дві відсортовані підпослідовності і так доти, доки основна черга не стане порожньою. Після цього послідовність з тимчасової черги переміщається в основну чергу. І знову продовжується сортування злиттям двох відсортованих підпослідовностей. Сортування триватиме доти, доки довжина відсортованої підпослідовності не стане рівною довжині самої послідовності. Наприклад: