Лекція 14. Хеш-таблиці. Дерева та префіксні дерева
1. Хеш-таблиці
Подивимось на ці сині зошити, кожен з них помічено буквою алфавіту. Якби їх було перемішано і ми повинні були би розсортувати їх, ми інстинктивно почали би складати їх до купи згідно першої літери, а потім сортували би кожну купу окремо.
Ідея в тому, що ми дивимось на вхідні дані та приймаємо рішення згідно цих даних (A відправляється до цієї купи, Z — до іншої). Ця техніка називається хешуванням — це коли на основі вхідних даних обчислюється величина, у більшості випадків число, яке стає індексом, наприклад, у масиві.
Ми можемо помітити А як 0, а Z як 25 і таким чином помістити їх до відповідної купи.
Програма на С може просто використовувати ASCII-значення, проте віднявши 65 від великої A або 97 від маленької a, ми зможемо помістити їх у комірку з індексом 0.
Насправді, таким чином ми перевіряємо тести: розкладаємо їх по купах, сортованих по імені куратора, щоб кожен куратор міг з легкістю знайти роботи своїх студентів.
Протягом минулорічного хакатону, ми розсортували бейджі за алфавітом, щоб ті, хто вітав учасників, могли би з легкістю їх знайти.
Один з кураторів створив дуже дотепне оголошення — “Хешуйтесь (за іменами)”.
Давайте формалізуємо цю ідею. На рисунку зображено масив з індексами рядків зліва:
 Масив має 26 елементів та ім'я table.
Масив має 26 елементів та ім'я table.
Це одна з можливих імплементацій хеш-таблиці, високорівневої структури даних, яка може використовувати масив або зв'язний список, або інші інгредієнти, щоб отримати більш корисні фінальні результати.
Ми можемо створити хеш-таблицю наступним чином: char* table[CAPACITY]; у цьому випадку це буде масив із розміром CAPACITY, але ми можемо сказати, що хеш-таблиця — це абстрактний тип даних, який створено на основі цього масиву.
Раніше ми використовували справжній стіл (гра слів: і стіл, і таблиця — це table — прим. пер.), щоб розкласти купи синіх зошитів відповідно до літер алфавіту. Але стіл має фіксований розмір, і якщо би ми мали два елементи з однаковим номером, ми би не мали місця куди їх покласти, крім як один на одний, як у справжньому масиві.
То ж ми можемо помістити один з елементів на інше місце, туди, де мав би бути зошит із літерою B. Але в такому разі B піде нижче і це може стати проблемою, але така техніка є, і вона зветься лінійним дослідженням — ми дивимось на кожний елемент у масиві та шукаємо місце, щоб покласти наступний елемент.
Вставка починається на складності Ο(1), бо спочатку масив порожній, та ви можете перейти до необхідної комірки миттєво, але як тільки дані зростають, вставка починає коштувати часΟ, тому що ми маємо пройти крізь масив, щоб знайти потрібне місце для вставки. Якщо масив доволі великий, та дані не дуже щільні, ви маєте всі переваги сталого часу, але все ж є ризик і це робить лінійне дослідження недосконалим.
2. Дерева та префіксні дерева
Замість хеш-таблиці ми можемо використовувати дерево, на кшталт генеалогічного дерева. Якщо ми почнемо з порожнього дерева, ми можемо створити вузол, який має виглядати десь так:
|
|
|
|
……………. |
Кожній комірці у цьому прямокутнику (який складається за 26 елементів) призначено літеру алфавіту. Тож виходить, що перша комірка — це літера “A”, друга — це “B” і так далі.
Якщо би ми хотіли вставити ім'я “DAVEN”, ми би мали спершу захешувати його та усвідомити, що воно починається з літери “D”. Але ми не можемо помістити все ім'я до прямокутника, тож ми збудуємо інші вузли для кожної літери й встановимо вказівники на кожну літеру кожного вузла.
Щодо останньої літери ім'я Daven, якщо ми не хочемо використовувати NULL (все ж таки Daven це скорочене Davenport, а ми хочемо, щоб обидва рядки були валідні), то ми маємо розділити кожну комірку на дві. Ось тут намальовано останню комірку, зазначену n — вона вміщує два поля. Ми можемо використовувати верхнє, як сигнал до того, що це кінець рядку й нижнє поле хай буде вказівником:
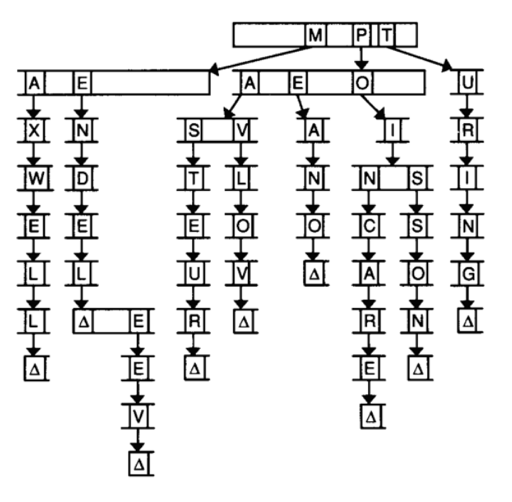
Кожен з прямокутників має 27 індексів, адже ми хочемо використовувати апострофи.
Ми будемо називати цю структуру префіксне дерево або trie (trie — це таке дотепне ім'я для дерева, що оптимізоване для пошуку — reTRIEval, вимовляється як “трай”) .
Ці префіксні дерева використовують багато пам'яті, адже кожен вузол виділяє місце для багатьох індексів, й більшість з цих місць буде порожня, принаймні спочатку, коли в нас є лише декілька рядків.
Але ми отримуємо швидкість та витрачаємо менше часу, адже час вставки дорівнює Ο(1), бо не існує нескінченно довгих імен. Найдовше слово у словнику цього практичного завдання матиме 40 літер, але це буде стала величина, яка не залежатиме від інших імен у цій структурі. Щодо часу виконання, він залежатиме від довжини рядка, яка асимптотично сягає Ο(1).
Ми можемо реалізувати це в наступний спосіб:
typedef struct node
{
bool word;
struct node* children[27];
}
node;
node* trie;
Кожен вузол node матиме булеве значення bool, яке відповідатиме за кінець слова та масив із 27 вказівниками на інші вузли.
Щоб оголосити наше префіксне дерево, ми повинні мати один node*, що вказує на кореневий елемент, як у в зв'язних списках.
Подивимось на наш малюнок: якщо би ми хотіли вставити ім'я “Dave”, все що ми б мали зробити — це простежити за вказівниками та змінити комірку, що відповідає за закінчення слова: